Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
График функции y = kx^2
Вступление
Давайте рассмотрим еще один вид функции график x в квадрате с коэффициентом. Так как опыт построения графика функции x в квадрате у нас уже есть, то и с коэффициентом мы легко разберемся. Давайте узнаем, в чем сходство этих функций. Какое название носит график функции x в квадрате с коэффициентом. Какими важными свойства он обладает. Обо всем мы узнаем на сегодняшнем занятии.
Теория по теме Функция y = kx^2, ее свойства и график
Заметим, что функция y=kx{|pow|2|} очень похожа на функцию y=x{|pow|2|}2, которую мы уже строили. График функций такого рода (при k≠0) называется параболой.
Функция y=x{|pow|2|} является частным случаем функции y=kx{|pow|2|}, при k=1, соответственно их графики будут весьма схожи.
Построим график функции y=kx{|pow|2|} таким же способом, как и строили график функции x в квадрате.
Допустим, необходимо построить график функции y=kx{|pow|2|} при k=3, функция будет иметь вид: y=3x{|pow|2|}.
Вычислим координаты некоторых точек, которые принадлежат данной функции.
y=3x{|pow|2|}
x | 0 | 1 | 2 | -1 | -2 |
y | 0 | 3 | 12 | 3 | 12 |
Построим график функции, соединив точки.
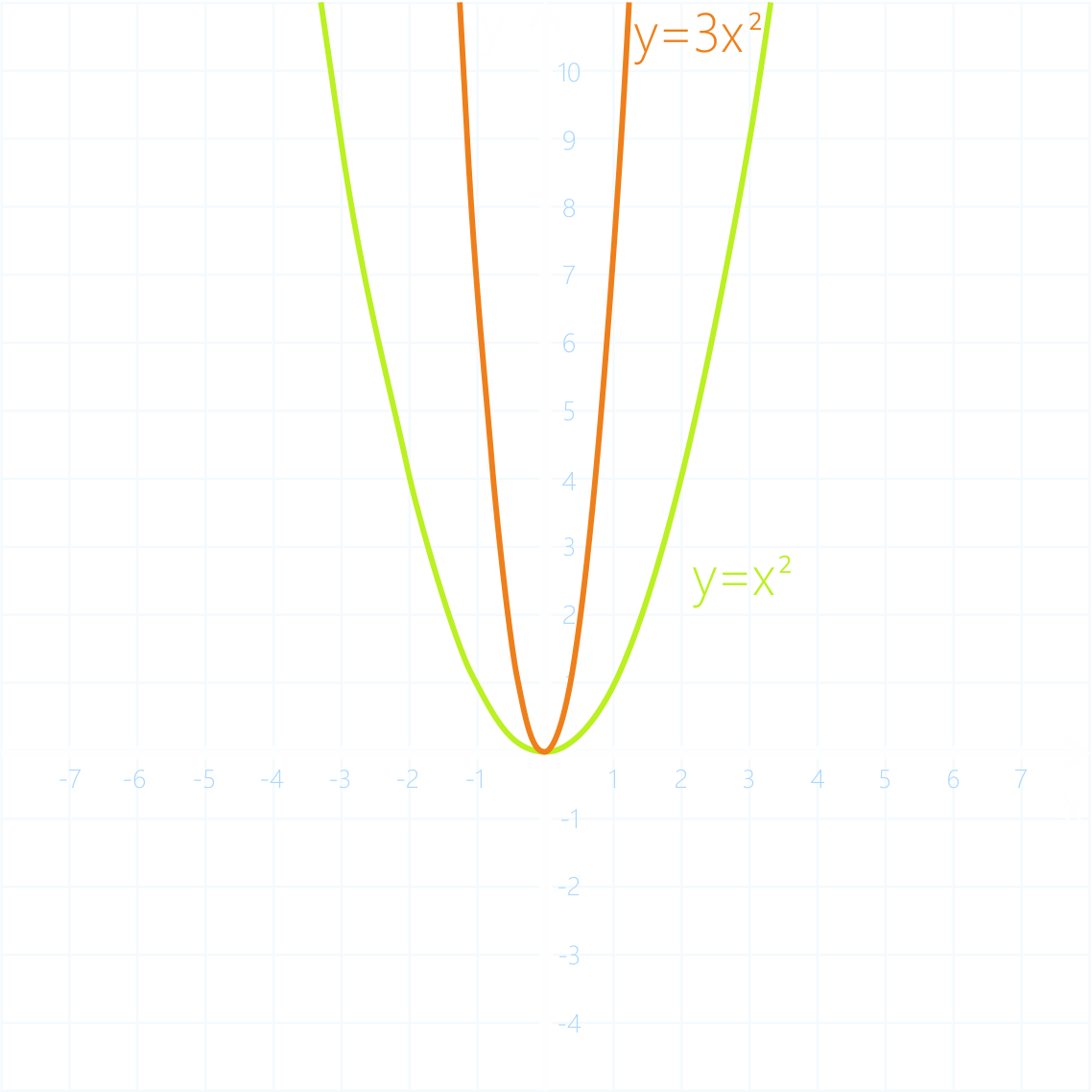
Заметим, что точка (0;0) является “началом” параболы, в данном случае говорят, что это вершина параболы. Также обратим внимание, что парабола симметрична относительно оси y. Две линии графика, расположенные слева и справа от вершины параболы называются ветвями параболы.
Определение. Графиком функции y=kx{|pow|2|} (k≠0) является парабола, вершина которой находится в точке (0;0), при k>0, ветви параболы направлены вверх, при k<0 , ветви параболы направлены вниз.
Свойства функции y=kx{|pow|2|} (k≠0):
- область определения функции: (-{|inf|};+{|inf|}), т.е. все значения переменной x, при которых функция определена;
- функция непрерывна, т.е. график функции представляет собой непрерывную линию;
- при k>0: y{|index|min|}=0, y{|index|max|} отсутствует;
- при k<0: y{|index|min|} отсутствует, y{|index|max|}=0;
- при k>0: функция убывает при x<0, возрастает при x>0, при k<0: функция возрастает при x<0, убывает при x>0;
- область значений функции: при k>0: [0;+{|inf|}), при k<0: [0;-{|inf|}).
Заключение
Как мы узнали из сегодняшнего занятия, график функции x в квадрате с коэффициентом k носит название парабола. У каждой параболы есть вершина и две ветви, которые расположены симметрично относительно оси ординат. Чтобы построить параболу, мы вычислили координаты некоторых точек, принадлежащих графику x в квадрате, и соединили их линией. Говоря о свойствах этого графика можно легко заметить, что все они визуализированы на координатной плоскости. Поэтому не старайтесь бездумно заучивать свойства функций, постарайтесь вникнуть и увидеть отображение каждого свойства на рисунке графика. Тогда Вы сможете без лишних усилить запомнить все свойства функции х квадрат. А сейчас пришло время потренироваться. Нажимайте кнопку решать и переходите к заданиям, которые подготовил для Вас Виртуальный Учитель.
0
Аккаунт
Учёба
Статистика
