Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Формулы сокращенного умножения. Квадрат суммы и квадрат разности
Вступление
Сегодня мы рассмотрим еще две формулы - квадрат суммы и квадрат разницы. Они часто будет встречаться нам в выражениях. Где, например, нам могут пригодиться эти формулы? Мы будем встречаться с примерами и задачами, в которых нужно упростить выражение, раскрыть скобки, свести подобные и т.д. В таких случаях нужно применять формулы, в том числе квадрат разности и квадрат суммы. Чем больше формул Вы знаете, тем интереснее и увлекательнее решение выражений, ведь Вы сможете проанализировать пример и применить к нему максимальное количество формул, тем самым упростить его и решить в кратчайший срок. Запомните, что формулы на квадрат суммы и квадрат разности имеет правую и левую стороны, обе равноправно применимы в решении выражений. Вам следует быть внимательными и анализировать, какой вариант преобразования выражения в дальнейшем упростит решение выражения? Именно его и выбирайте.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Квадрат суммы и квадрат разности
Формула квадрата суммы чисел является одной из основных в формулах сокращенного умножения. Данная формула применяется в основном при разложении выражения на множители.
Формула квадрата суммы двух чисел:
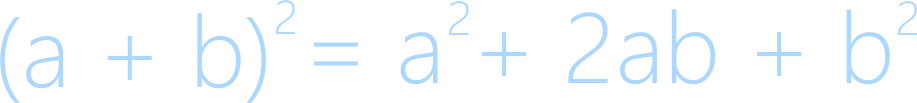
Квадрат суммы
Запомните формулу квадрата суммы и обратите внимание на слагаемое 2ab, так как его очень часто забывают, тем самым допуская довольно грубую ошибку.
Важно:
(a+b){|pow|2|}≠a{|pow|2|}+b{|pow|2|}
Другими словами, квадрат суммы равен сумме квадрата первого числа с квадратом второго числа и с удвоенным произведением этих чисел.
Квадрат суммы применяется не только для двух чисел, но и для трех и больше.
Кроме как для двух чисел, чаще всего применяют квадрат суммы трех чисел.
Формула квадрата суммы трех чисел:
(a+b+c){|pow|2|}=a{|pow|2|}+b{|pow|2|}+c{|pow|2|}+2ab+2ac+2bc
Таким образом, квадрат суммы нескольких чисел равен сумме квадратов чисел и их удвоенных попарных произведений.
Квадрат разности является близкой формулой к квадрату суммы, таким образом, данную формулу, в основном, используют при необходимости разложения выражения на множители или более быстрого раскрытия скобок и приведения подобных.
Формула квадрата разности:
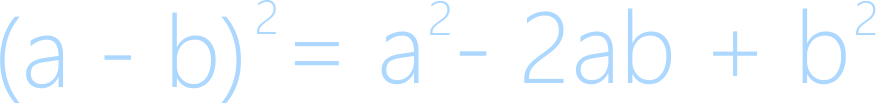
Квадрат разности
Обратите внимание на важный член формулы разности квадратов - 2ab, и не забывайте данную часть при использовании квадрата разности, а также обратите внимание на то, что, формула квадрата разности похожа на формулу квадрата суммы и отличается лишь знаком среднего члена.
Важно:
(a-b){|pow|2|}≠a{|pow|2|}-b{|pow|2|}
То есть квадрат разности двух чисел не равен разности квадратов двух чисел.
Таким образом, квадрат разности двух чисел равен квадрату суммы, с одним лишь отличием в знаке удвоенного произведения чисел.
Вместо букв в задачах и примерах часто встречаются числа. Но не стоит сомневаться в возможности применения формулы, ведь квадрат разности чисел работает как с буквами, как и со всем, что можно написать вместо них, например, с числами.
Заключение
Сегодня мы изучили квадрат суммы и квадрат разности. Рассмотрели формулы квадрата разности и квадрата суммы, узнали, что оны применимы не только к двум числам, но к трем и более. Обратили внимания на ошибку, которая часто допускается при применении формул. Будьте внимательны и помните об удвоенном произведении чисел. Для того чтобы закрепить полученные знания, нужно потренироваться решать на практике примеры на квадрат суммы и квадрат разности. Для этого Виртуальный Учитель уже подготовил Вам подборку примеров. Нажимайте решать и переходите к заданиям.
0
Аккаунт
Учёба
Статистика
