Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Функция y = k/x
Вступление
Сегодня нас ждет знакомство с еще одним видом функции под названием гипербола. Это функция к деленное на х. Мы выберем значение коэффициента, вычислим значения переменных, построим график гиперболы и определим все его свойства и особенности. Этот алгоритм действий будет неизменным при изучении графиков функций. Именно таким образом мы сможем проанализировать полученный график, и на основе изображения описать свойства функции k деленное на x. Итак, приступим к изучению данной функции.
Теория по теме Функция y =k / x, ее свойства и график
Рассмотрим новый для нас график функции y={|frac|k|x|} (k≠0). Построим данный график уже привычным для нас способом - по точкам.
В качестве конкретного значения коэффициента k возьмем, например, 2.
Найдем координаты некоторых точек, принадлежащих графику.
y={|frac|2|x|}
x | 1 | 2 | 0,5 | -1 | -2 | -0,5 |
y | 2 | 1 | 4 | -2 | -1 | -4 |
Заметим, что при x=0, функция не определена (т.к. нельзя делить на нуль), поэтому при x=0 происходит разрыв функции.
Построим график функции, отметив точки и соединив их.
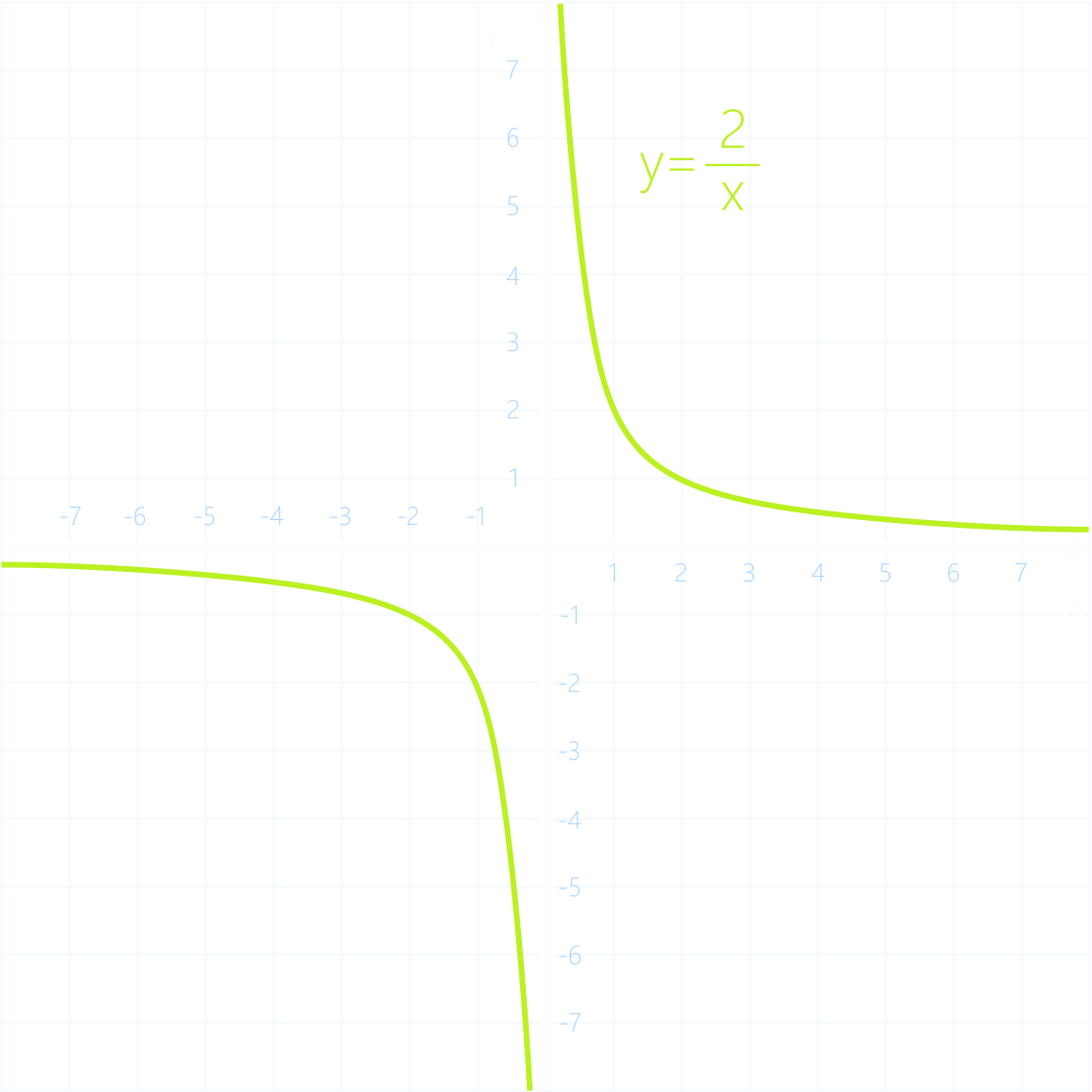
Гипербола. График функции 2/х.
Построенный нами график функции называется гипербола.
Как мы заметили ранее, гипербола, график которой мы построили, состоит из двух частей, их называют ветвями гиперболы.
Из построенного графика видно, что ветви гиперболы прижимаются (стремятся) к двум прямым: оси абсцисс, оси ординат. Прямые, к которым стремятся ветви гиперболы называются асимптотами.
Гипербола, график функции которой состоит из двух ветвей, может выглядеть по-разному, в зависимости от коэффициента k.
В случае, когда k>0, график гиперболы имеет ветви, расположенные в 1 и 3 четверти плоскости, а когда k<0, график гиперболы имеет ветви, расположенные во 2 и 4 четверти координатной плоскости.
Свойства функции y={|frac|2|x|}:
- область определения функции: (-{|inf|};0) {|U|} (0;+{|inf|});
- при k>0: функция убывает при x<0 и убывает при x>0,при k<0: функция возрастает при x<0 и возрастает при x>0;
- y{|index|min|} - не существует, y{|index|max|} - не существует;
- функция непрерывна при x: (-{|inf|};0)и при x: (0;+{|inf|});
- область значений функции: (-{|inf|};0) {|U|} (0;+{|inf|}).
Заключение
Мы познакомились с новым видом функции - гиперболой. Научились строить ее график, узнали, как будет меняться вид графика гиперболы в зависимости от коэффициента. Свойства функции у равно k деленное на x понять достаточно просто, если построить график гиперболы при положительном и отрицательном коэффициенте. Мы можем наблюдать, как с изменением знака коэффициента функция отражается относительно оси абсцисс. Чтобы закрепить пройденный сегодня материал, переходите к заданиям от Виртуального Учителя. Нажимайте кнопку решать.
0
Аккаунт
Учёба
Статистика
