Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Основные понятия об алгебраических дробях
Вступление
Дроби имеют свои свойства. Эти свойства важно помнить, когда мы проводим математические операции с дробями. Часто знание свойств дробей значительно упрощает и рационализирует процесс решения выражения с дробями. Давайте сегодня рассмотрим основное свойство дроби алгебраической (рациональной), а затем потренируемся применять знание свойства дробей на практических примерах. Давайте начинать.
Теория по теме Основное свойство алгебраической (рациональной) дроби
Давайте вспомним, что алгебраическая, или как еще говорят, рациональная дробь это дробь, числитель и знаменатель которой представляют собой выражение с переменными. Также следует помнить, что знаменатель любой дроби не должен быть равен нулю.
Для начала вспомним основное свойство обычной дроби: при умножении и делении числителя и знаменателя дроби на одно и то же число получится дробь, равная исходной.
Данное правило работает и для алгебраической (рациональной) дроби, но сформулировать его можно в более общем случае.
Основное свойство алгебраической (рациональной) дроби: если числитель и знаменатель алгебраической (рациональной) дроби умножить или разделить на один и тот же ненулевой многочлен, то получится дробь, тождественно равная исходной.
Например, возьмём дробь {|frac|2|3|} и умножим числитель и знаменатель на 5.
Получим: {|frac|2*5|3*5|}={|frac|10|15|}.
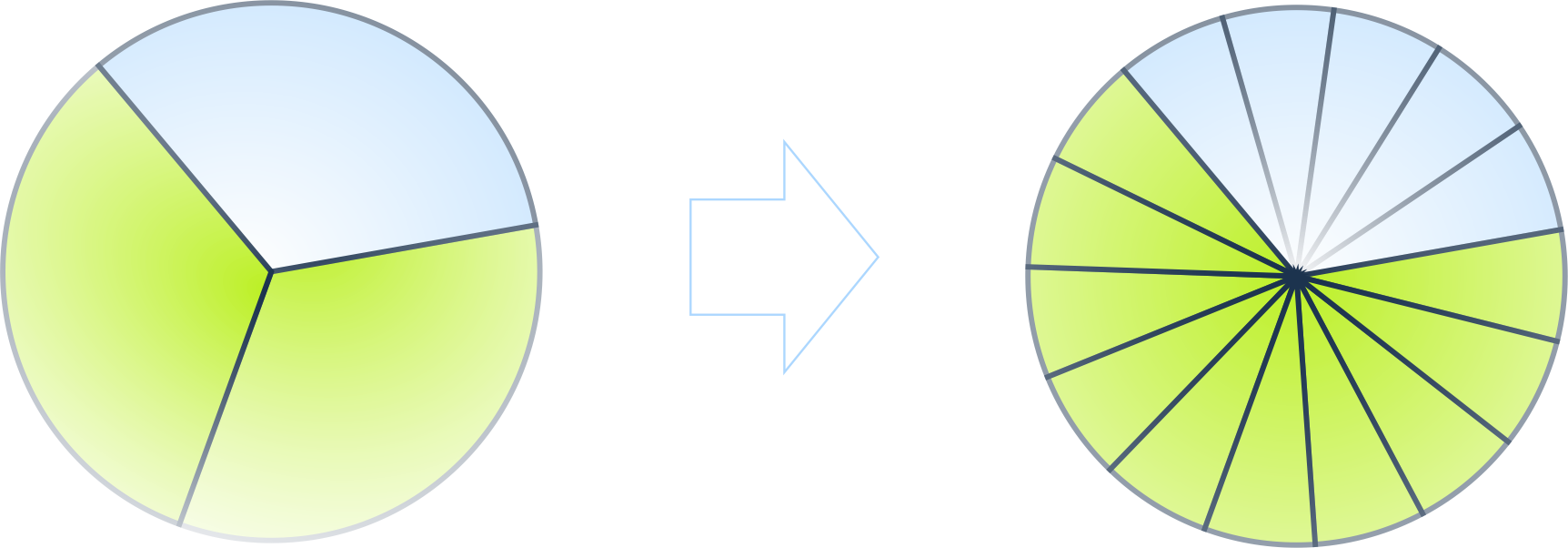
Как видно из ресунка, дроби {|frac|2|3|} и {|frac|10|15|} равны.
Аналогично при делении числителя и знаменателя на одно и тоже число мы получим равные дроби.
Напомним, что деление числителя и знаменателя дроби на один и тот же ненулевой многочлен, называется сокращением дроби.
Заключение
Как мы выяснили, основным свойством алгебраической дроби, которую еще называют рациональной, является свойство сокращения дроби. Одновременное деление или умножение числителя и знаменателя дроби на один и тот же многочлен дает нам большие возможности при решении сложных выражений. Пришло время потренироваться на практике применять основное свойство дроби и решить примеры, которые подготовил для Вас Виртуальный Учитель. Нажимайте кнопку решать.
К вашей цели с Виртуальным учителем
