Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Что такое степень с натуральным показателем
Вступление
Давайте узнаем, что такое степень с натуральным показателем? Для начала познакомимся с самим понятием степени. Узнаем, какие особенности имеет степень с натуральным показателем. Что называют основанием, а что показателем степени. Задания на возведение числа в степень с натуральным показателем регулярно встречаются в проверочных и контрольных работах. Нужно хорошо разобраться в ней, чтобы не допускать ошибок. Итак, начнём!
Теория по теме Степень с натуральным показателем
Разберем случаи, когда необходима более краткая запись. Например, когда дано выражение: 3*3*3*3. В случаях перемножения нескольких одинаковых множителей, существует альтернативная и более краткая запись такого выражения:
3*3*3*3=3{|pow|4|}, читается как: три в степени четыре.
То есть три в степени четыре означает перемножение четырех троек.
Степень с натуральным показателем - это число вида a{|pow|b|}, в котором b является натуральным числом. Под a{|pow|b|} понимают произведение b раз множителей, каждый из которых равен a.
Выражение a{|pow|b|} называют степенью с натуральным показателем,
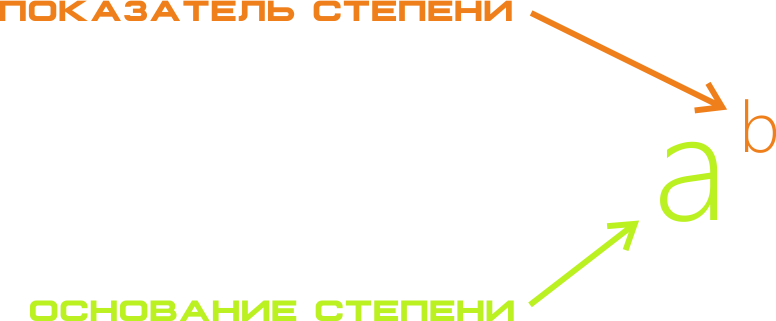
число a называют основанием степени,
число b называют показателем степени.
Получается, что степень с натуральным показателем является лишь краткой записью произведения одинаковых множителей, в некоторых случаях будет полезно степень с натуральным показателем представить через произведение множителей, а в других случаях наоборот представить произведение нескольких множителей через степень числа.
Заключение
Сегодня мы изучили тему степень с натуральным показателем. Узнали, что такое степень и каково её математическое выражение. Запомнили, что в выражении a{|pow|b|} число a будет основанием степени, а b - показателем степени. Давайте перейдём к практической части занятия и закрепим пройденный материал, проработав задания от Виртуального Учителя. Нажимайте решать.
0
Аккаунт
Учёба
Статистика
