Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Взаимное расположение графиков линейных функций
Вступление
Как мы помним, координатная плоскость возникла из-за потребности описывать местоположение тел в пространстве. У каждой точки тела на координатной плоскости есть точные координаты. А что, если это тело или фигура не одна? если их две или несколько. Тогда нам будет интересно описать их взаимное расположение, чтобы понять, совпадают ли они или пересекаются? А если это прямые, возможно, они расположены параллельно? Давайте разберём какие бывают виды взаимного расположения на примере графиков линейных функций, которые, как мы помним, представляют собой прямые.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Взаимное расположение графиков линейных функций
Рассмотрим любые две прямые на плоскости.
Прямые на плоскости могут:
- совпадать,
- пересекаться,
- быть параллельными.
Совпадают
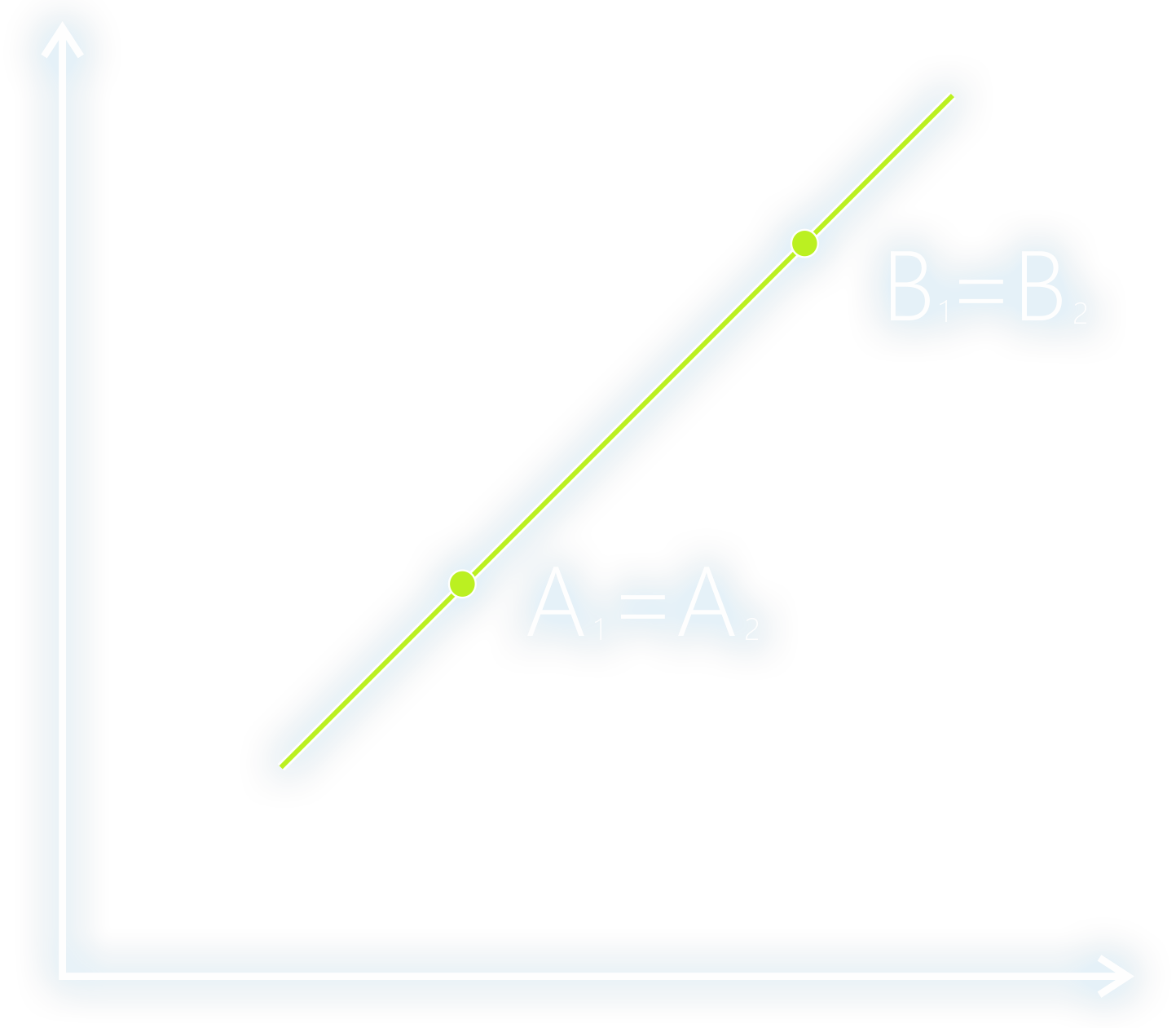
Прямые совпадают тогда, когда любая точка, принадлежащая первой прямой, принадлежит также и второй прямой.
Пересекаются
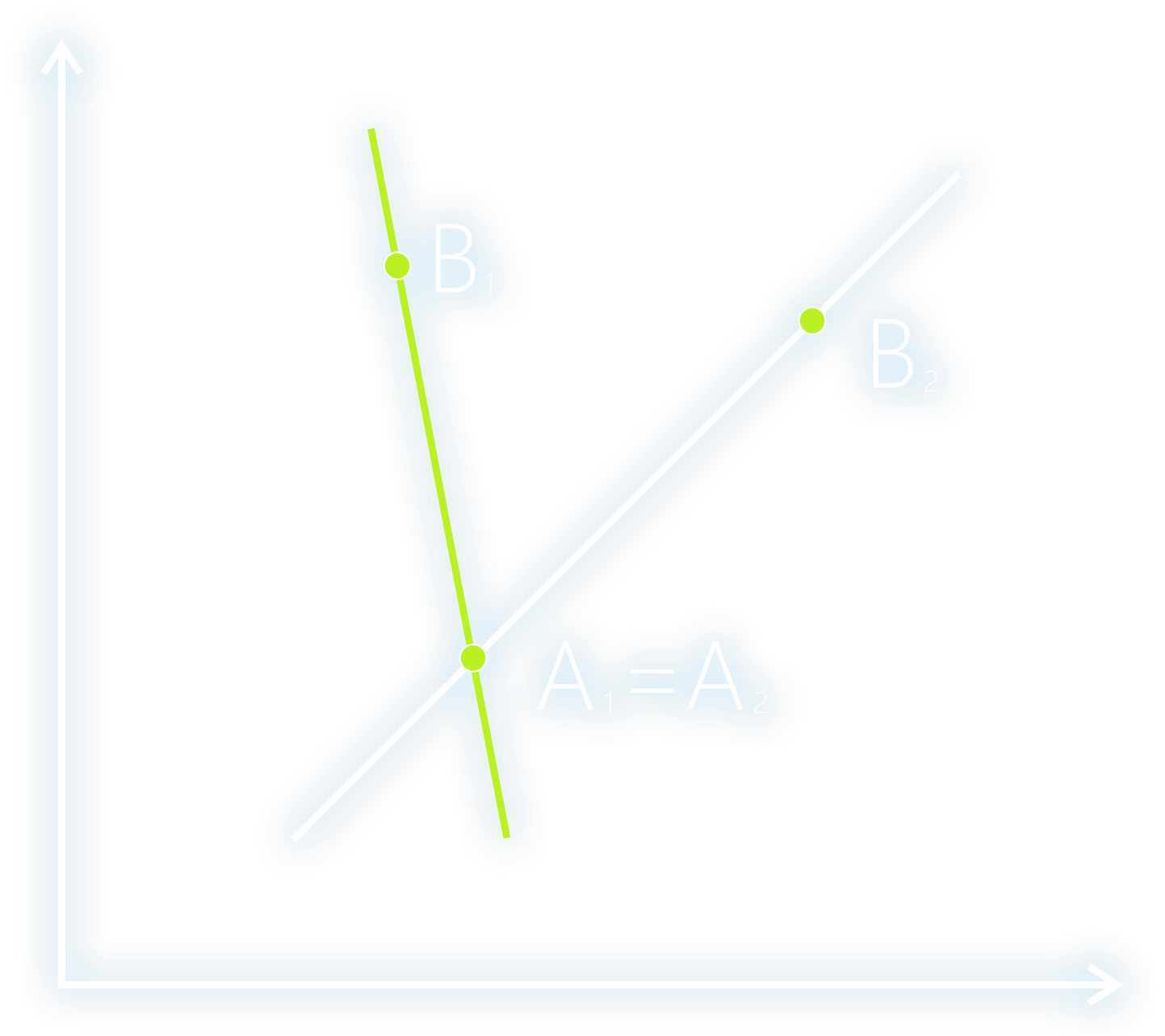
Прямые пересекаются тогда, когда они имеют ровно одну общую точку.
Параллельные
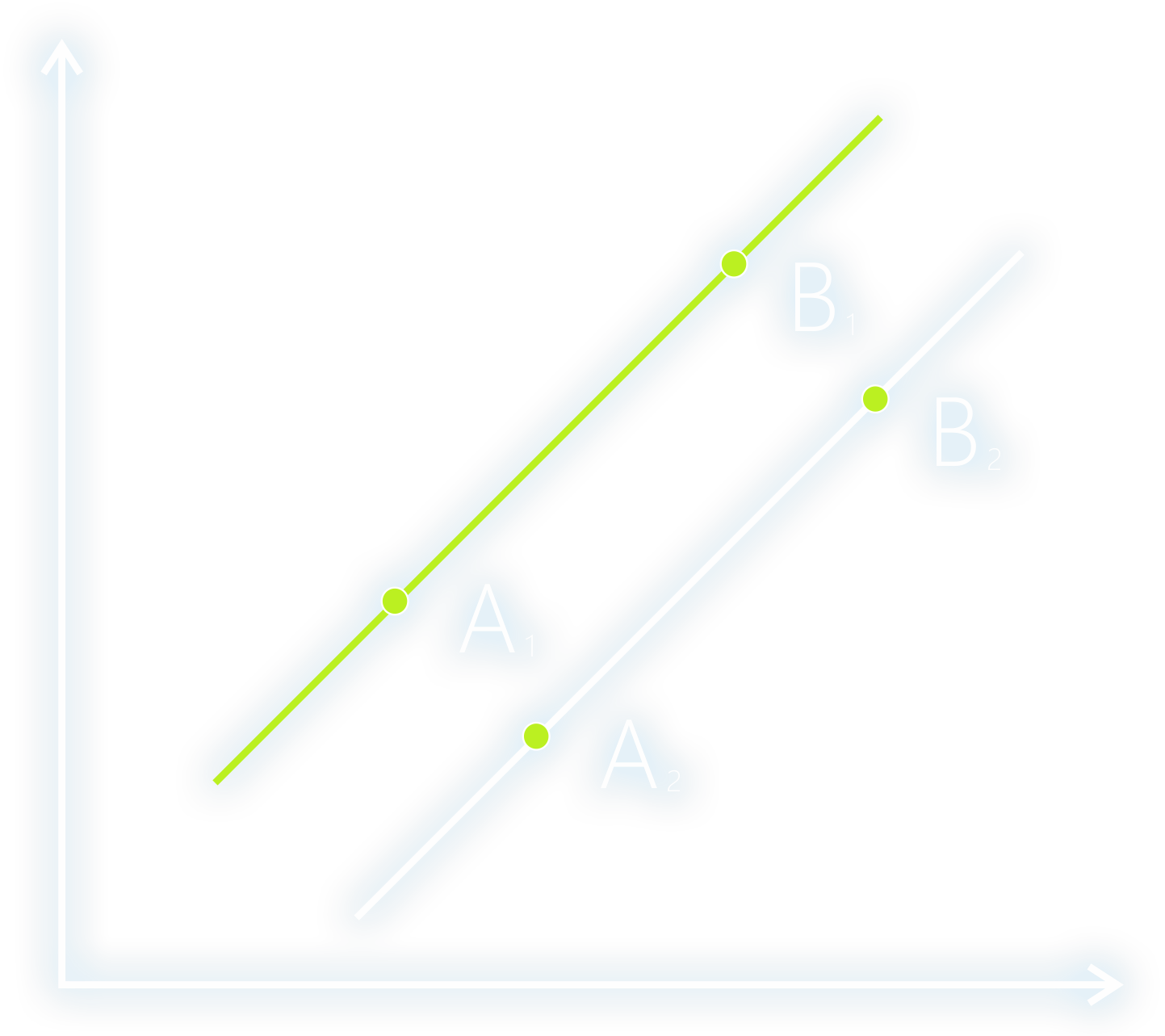
Прямые параллельны тогда, когда они не имеют общих точек, т.е. не пересекаются.
Так как графиком линейной функции является прямая, то можно говорить о взаимном расположении графиков линейных функций.
Правило: Графики двух линейных функций y=k{|index|1|}x+b{|index|1|} и y=k{|index|2|}x+b{|index|2|} по отношению друг к другу могут:
- совпадать, если k{|index|1|}=k{|index|2|} и b{|index|1|}=b{|index|2|},
- пересекаться, если k{|index|1|}≠k{|index|2|},
- быть параллельными, если k{|index|1|}=k{|index|2|} и b{|index|1|}≠b{|index|2|}.
Значит, если только угловые коэффициенты совпадают, то прямые параллельны, если все коэффициенты совпадают, то и сами прямые совпадают, во всех остальных случаях прямые пересекаются.
Чтобы установить взаимное расположение графиков линейных функций, необходимо сравнить их коэффициенты.
Например, прямые y=2x+3 и y=2x+5 параллельны, а прямые y=2x+4 и y=4x+2 пересекаются.
Заключение
Сегодня мы узнали, каким бывает взаимное положение графиков линейных функций. Они могут совпадать, пересекаться или быть параллельными друг другу. Как мы увидели, эти положения зависят от коэффициентов. Поэтому для каждого положения есть своё соотношение коэффициентов, которое мы детально рассмотрели в правиле. Теперь давайте потренируемся и выполним задания от Виртуального Учителя. Нажимайте кнопку решать.
К вашей цели с Виртуальным учителем
